Asking what an unsigned number or integer is, is actually asking, how to represent the non negative integers, such as 0, or 1 in a computer.

An integer in mathematics, is any number which belong to the set Z, where the set Z, is the set containing the positive whole numbers, such as : 1, the negative whole numbers such as : -1, and the number : 0.

What is an Unsigned number

Encoding in the computer, consists of representing data, using a string of bits, formed only of 0 and 1, such as 10101, called a binary representation. Binary as in the digits used, consist only of the two values 0, or 1.

This being said, representing, or encoding a number in a computer, can be performed using only a limited number of bits, for example 8, or 16, since a computer memory is limited.

As such, once the number of bits, to encode integer values, larger or equal to zero, has been chosen, only a limited set, of non negative integers, can be encoded. These non negative integers, with their encoding, are called unsigned integers, and they form an unsigned integer set.

In unsigned encoding, non negative integers, are encoded using, the binary positional numeral system. For example, the number 5, as written in the decimal positional numeral system, is written as 0101, in the binary positional numeral system. So for unsigned encoding, the value 0101, represents the encoding, of the non negative integer 5.

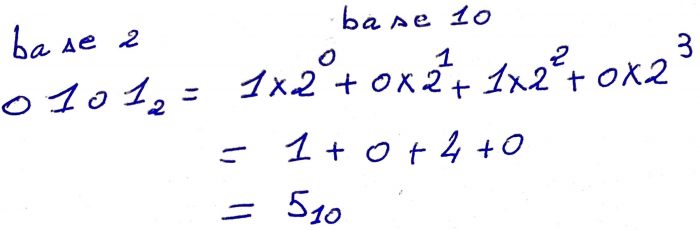
In a high level programming language, unsigned integers, are represented using a data type, for example in c or c++, unsigned integers, are represented using the following data types :

unsigned char 
# typically 8 bits.
# at least 8 bits.

unsigned short 
# typically 16 bits.
# at least 16 bits.

unsigned int 
# typically 32 bits.
# at least 16 bits.

unsigned long 
# typically 64 bits
# at least 32 bits.

unsigned long long 
# typically 64 bits
# at least 64 bits.

Having chosen a number of bits, and how to encode non negative integers in the computer, we end up with an unsigned integer set, formed of a limited number, of non negative integers, and their encodings, the question to ask hence, is what operations, can be performed on this set. This will be the subject of the discussion, in the next sections.

For the following sections, the set that we will be working with, to elucidate the operations that can be performed, has only two bits reserved for encoding, as such the unsigned integer set, that we will be working with, is :

Unsigned integer addition

Addition is performed, using the binary positional numeral system, as such it works like regular addition, with carry and so on.

A problem that is faced, when performing addition using unsigned integers, is that, there is a limited number of bits used for encoding. This can lead to overflow, which is that a result, is too large to be represented, using the chosen encoding.

When the result of an unsigned addition, is too large to be represented using the selected number of bits, the excessive bits are thrown away, so the resulting number of bits is truncated, to fit the selected number of bits. This is the same as :

As such , the result of performing unsigned integer addition, when the numbers of bits selected for encoding, is only 2, is :

To detect if unsigned integer addition overflow has occurred, it is sufficient to check, if the result of the unsigned addition, is smaller of any of its two operands.

int unsigned_addition_overflow( unsigned int x, unsigned int y ){
  /* Check if unsigned int addition overflow,
    will occur, return 1, if it does, 0 
    otherwise.*/ 
  return ( x + y )  < x;}  

Unsigned integer multiplication

Unsigned integer multiplication, works like regular multiplication, because it is being performed using base 2.

The problems faced by unsigned multiplication, are caused by the limited number of bits used, which lead to overflow.

For unsigned integer multiplication, when overflow occurs, the exceeding bits are thrown away, and the result is truncated to the selected number of bits. This is the same as :

As an example, a table of unsigned multiplication, when encoding is performed using two bits is :

To detect unsigned multiplication overflow in C, it can be done using this method, or one of its derivatives.

#include<limits.h>
/* The limits.h header contains the
   min and  max values, that integer
   types in C, can have on a certain
   machine. */

int unsigned_multiplication_overflow( unsigned char x, unsigned char y ){
  //Check for unsigned char multiplication overflow 
  if( x == 0 || y == 0 )
    return 0; //no unsigned char multiplication overflow
  if( x == 1 || y == 1 )
    return 0; // no unsigned char multiplication overflow
  unsigned char z = UCHAR_MAX / x ;
  /* Perform unsigned division,
     For example, x = 20, UCHAR_MAX = 255
       z = 12.
     z is the greatest number such that :
       z * x <= UCHAR_MAX */
  if( y > z )
    return 1;//unsigned char multiplication overflow
  else
    return 0; /*no unsigned char multiplication overflow*/}

Unsigned integer division

Unsigned integer division, works the same as regular integer division, since the division is being performed using base 2. It returns only the quotient, without any remainder or fractional part.

No overflow can occur while performing unsigned integer division, and the result of dividing by 0 is undefined.

Unsigned integers subtraction

When subtracting, the larger unsigned value, from the smaller unsigned value, the result is correct, but when subtracting the smaller unsigned value, from the larger unsigned value, the result is negative.

The formula to compute the result, when the subtraction of two unsigned integers, yield a negative value, is the following :

As an example, the following tables, details unsigned subtraction, using 2 bits :

To check if the subtraction of two unsigned integers, will yield a modulo result , this can be done as follows :

int unsigned_substraction_modulo( unsigned char x, unsigned char y ){
  // Check if y - x cause modulo result. 
  if( x <= y )
    return 0; // no unsigned char substraction modulo result
  else
    return 1;/* unsigned char substraction modulo result */}

Commutativity, associativity, and distributivity

unsigned addition 
    commutative : a + b = b + a 
    associative : a + ( b + c ) = ( a + b ) + c 


unsigned Multiplication
    commutative : a * b = b * a 
    associative : a * ( b * c ) = ( a * b ) * c 
    distributive over addition and substraction 
                  a * ( b + c ) = ( a * b ) + ( a * c )
                  a * ( b - c ) = ( a * b ) - ( a * c )


unsigned Division
    not commutative  : ( 1 / 2 ) != ( 2 / 1 )
    not associative  : ( 1 / 2 ) / 3 != 1 / ( 2 / 3 ) 
                  because     0      !=   undefined 


unsigned Subtraction
    not commutative : 1 - 2 != 2 - 1  
    not associative : ( 1 - 2 ) - 1 != 1 - ( 2 - 1 )