A number , can be thought of as a projection , used for example for measuring , be it time or distance , or for countig . A number is a discrete way of measuring , discrete as in opposed to continuous , which can be useful under certain condition .

In mathematics multiple kind of numbers exist . There are for example , the nonnegative whole numbers , such as 0 or 1 , and which are represented by the set N .

There are the integer numbers which are formed of : 0 , the negative whole numbers such as -1 or -2 , and the positive whole numbers . The integer numbers are represented by the set Z .

There is also , the rational numbers , of the form p/q , where p and q are integers , and q is different from 0 . Rational numbers are represented by the set Q .

Numbers are represented in the computer , by using an algorithm . The set N is represented by using the unsigned number representation , the set Z is represented by using the signed number representation , and the set Q is represented using the floating point number representation .

Limitations of positional numeral systems

Some numbers cannot be represented using a finite sequence of fractional digits , in a positional numeral system .

Irrational numbers , such as pi , simply cannot be represented using a finite sequence of digits , in a positional numeral system .

Rational numbers of the form p/q , cannot be represented using a limited sequence of fractional digits such as .12 , when the chosen base , or the base multiplied by 1,2 ... q-1 is not divisible by q .

As an example 1/4 can be represented in the decimal positional numeral system , because 10 * 2 is divisible by 4 , as such 1/4 can be written in the decimal positional numeral system , as 0.25 .

1/3 is representable in the ternary positional numeral system , because when borrowing in this case , we are borrowing multiples of 3 , so 1/3 can be written as 0.1 , in base 3 .

1/3 has a repeating representation in the decimal positional numeral system , because 10 * 1 , and 10 * 2 are not divisible by 3 . As such 1/3 is represented in the decimal positional numeral system , as the repeating sequence 0.33333... .

It can be proven that any repeating fractional number , can be written as a rational number , for example :

Problems arise , when limiting the fractional part of a number in a positional numeral system , to a limited number of digits .

When the number of digits is limited , this means that only a limited number of fractional values can be generated . The question hence to ask , is how to represent non generated fractional values , is it by one of the generated values , or by just stating it cannot be represented .

Let’s take as an example , the set of fractional parts generated in base 2 , when limiting the number of fractional bits to three .

0.1 in base 10 , has the following representation in base 2 .

0.1 is smaller than any nonzero value , in the selected base 2 subset , which has a limited number of fractional digits , as such it cannot be represented in this subset . This is called an underflow .

Larger values , such as values larger than 0.1 , and which are not present in the generated set , can only be represented by approximation . 0.4 for example , can be represented as .011 which is equal to 0.375 in decimal . The difference between the stored value , and the actual value is as such : 0.4 - 0.375 , which is equal to 0.025 .

The stored value of 0.77 , when subtracted from the stored value of 0.57 , is equal to .110 - .100 , which is equal to .010 . The stored value of 0.3 is .010 , as such in our representation of the fractional parts in base 2 , 0.77 - 0.57 is equal to 0.3 and is not equal to 0.2 .

Adding more bits to the fractional part , will improve the precision of the represented numbers , and of the calculations . For example , when 4 bits are used for the fractional part , 0.1 in decimal can be represented as 0.0001 in binary .

Even with a wider number of digits , the problems discussed earlier will always persist . Some numbers cannot be represented accurately using a limited number of digits , such as the irrational , and having a limited number of digits , a limited number of fractional parts is available, as such a limited precision .

IEEE floating point format

When using the IEEE floating point number representation , in addition to the precision , which is the number of bits selected for the fractional part , there is the sign bits , and the exponent bits .

What this means , is that additional values can be generated , because of the presence of the exponent , and the sign bits , so simply put , this is just a way to improve the precision .

An IEEE floating point number , has a bit representation , and a numerical value . The IEEE specified the bit format that a floating point number must have , and by which its numerical value is to be interpreted . This bit format can be put to work or accustomed to different word length . A word is formed of a number of bits , so this format can be put to work on 32 bits , 64 bits , 128 bits and so on … It just works the same.

A single precision floating point number has a 32 bit representation , a double precision floating point number has a 64 bit representation , and a quadruple precision floating point number has a 128 bits representation .

Infinite values

When the exponent bits are set all to 1 , and the precision bits are set all to 0 , the floating point number bits sequence , represent an infinite value .

There are two infinite values , positive and negative infinity . When the sign bit is 0 , this is positive infinity , when the sign bit is 1 , this is negative infinity .

Infinity can be caused for example , when dividing a nonzero number by 0 , or when the result of an operation , after rounding has the infinite value .

Not A Number value

When the exponent bits are all set to 1 , and the precision bits are set to anything but 0 , the bit sequence , of the floating point number , represents NAN .

The value NAN , means not a number , and it can happen for example , when dividing 0 by 0 , or when adding positive and negative infinity .

There is no negative or positive NAN , so the sign bit does not matter .

Denormalized values

When the exponent bits are all set to 0 , the floating point number is in what is called a denormalized form .

The rational value of the floating point number , is equal , to the sign value , multiplied by 2 to the exponent value , multiplied by the precision value .

The sign value is either 1 , if the sign bit value is 0 or -1, if the sign bit value is 1 .

The exponent value is calculated using the formula 1 - bias . The bias is calculated using the formula :

The precision value is the same as the precision bits value . The precision bits value is calculated as a fractional positional binary number .

To illustrate this , let us say , that the floating points are encoded using 7 bits . 1 bit is a sign bit , 3 bits are exponent bits , and 3 bits are precision bits .

The sign value is equal to 1 , when the sign bit is 0 , and to -1 when the sign bit is 1 .

The exponent value is equal to 1 - bias , which is equal to -2 .

The precision bits values are , calculated as positional binary fractions .

The precision values are the same as the precision bits values .

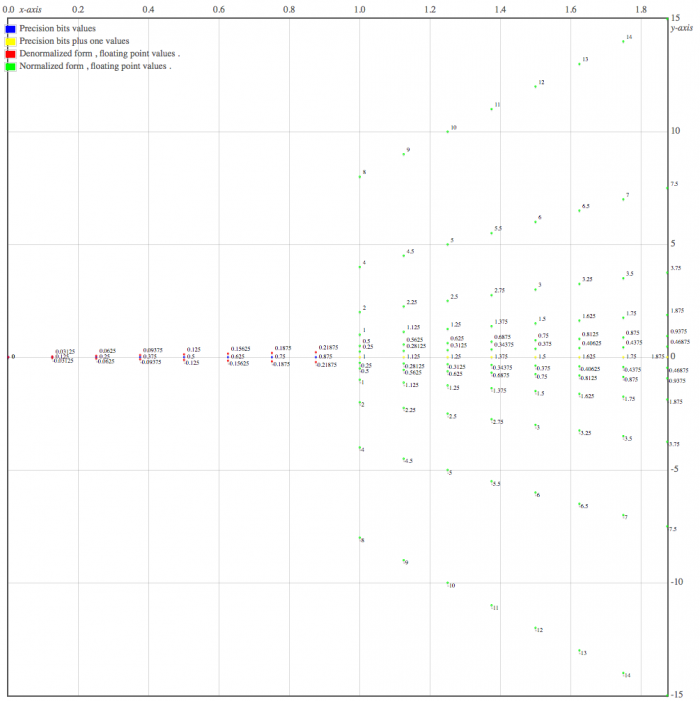
As such when in denormalized form , the 7 bits floating point numbers , possible rational values are :

Normalized values

When the exponent bits are not all set to 0 , or are not all set to 1 , the floating point number bits , are in normalized form .

The floating point number rational values , are equal to the sign value , multiplied by two to the power of the exponent value , multiplied by the precision value .

The sign value , is equal to 1 , when the sign bit is 0 , and is equal to -1 , when the sign bit is set to 1 .

The exponent value , is equal to the exponent bits values , minus the bias . The exponent bits values , are calculated , as if the exponent bits are in the binary positional numeral system . The bias is calculated as it was calculated in denormalized form .

The precision values , is equal to one , plus the precision bits values . The precision bits values , are calculated as if the precision bits , are a fractional base two number .

To illustrate this , let’s say that the floating point number is encoded using 7 bits . 1 bit is used for the sign , 3 bits are used for the exponent , and 3 bits are used for the precision .

The sign value is equal to 1 , when the sign bit is 0 , and -1 when the sign bit is 1 .

The possible exponent values are :

The possible precision values are :

The 7 bits floating point number , possible normalized form rational values are :

Visualizing floating points possible values , when the encoding is done on 7 bits

Commutativity , associativity , and distributivity

IEEE floating point addition 
    commutative : a + b = b + a 
    not associative : ( 5 + 1e40  )  - 1e40 != 5 + ( 1e40    - 1e40 )
                  because               0   !=  5 


IEEE floating point multiplication 
    commutative : a * b = b * a 
    not associative : 1e40 * ( 1e300 * 1e-300 ) != ( 1e40 *  1e300 ) * 1e-300 
                  because             1e40      !=   Infinity
    not distributive over addition and subtraction 
                  0 * (1e308 + 1e308 ) != ( 0 * 1e308 )  + ( 0 * 1e308 )
                  because          NaN != 0
                  1e30 * ( 1e300 - 1e300 ) != 1e30 * 1e300 - 1e200 *1e300
                  because        0         !=   NaN


IEEE floating point division 
    not commutative  : ( 1.0 / 2 ) != ( 2.0 / 1 ) 
    not associative  : ( 1.0 / 2 ) / 3 != 1 / ( 2.0 / 3 )  
                  because     0.1666 !=   1.5 


IEEE floating point subtraction 
    not commutative : 1.0 - 2 != 2 - 1.0  
    not associative : -4 - ( -4 - -3.0 ) != ( -4 - -4.0 ) - -3
          -4 - ( -4 - -3 )   = -4 - -1 = -3 
          ( -4 - -4 ) - -3 = 0 - -3 = 3 

Floating points format in C

Floating point formats are used to represent real , or rational numbers , in the computer . The C standard has three data types to be used with a floating point standard , they are : float , double , and long double .

The c standard , does not specify which floating point standard is to be used , but usually , the IEEE floating point format is used , as such float is mapped to the IEEE single precision floating point format , and double is mapped to the IEEE double precision floating point format .

By default a floating point literal such as 1.0 , has the type double , unless suffixed with f , in which case it will have the type float , or suffixed with l , in which case it will have the type long double .

To detect if a floating point value is NaN , it can be done by using the isnan function , and to detect if a floating point number is infinity it can be done using the isinf function .

The isnan , and isinf functions are both defined in the math.h header .

#include<stdio.h>
#include<math.h>

int main ( void ){
  printf( "%d\n", isnan( 0.0/0.0 ) );
  /* 0.0 divided by 0.0 , results in
     not a number , as such isnan
     returns a nonzero value . */
  // Output : 1
  printf( "%d\n" , isinf( 1.0/0.0 ) );
  /* 1.0 divided by 0.0 results in
     + infinity , as such isinf
     returns a nonzero value  */
  // Output : 1
}