A number , can be thought of as a projection , used for example
for measuring , be it time or distance , or for countig . A number is a discrete way of measuring ,
discrete as in opposed to continuous , which can be useful under certain condition .
In mathematics multiple kind of numbers exist . There are for
example , the nonnegative whole numbers , such as 0 or 1 , and
which are represented by the set N .
There are the integer numbers which are formed of : 0 , the negative whole
numbers such as -1 or -2 , and the positive whole numbers . The integer numbers
are represented by the set Z .
There is also , the rational numbers , of the form p/q , where p and q are
integers , and q is different from 0 . Rational numbers are represented by the set
Q .
Numbers are represented in the computer , by using an algorithm . The set
N is represented by using the unsigned number representation ,
the set Z is represented by using the signed number representation , and
the set Q is represented using the floating point number representation .
Table of Contents
Limitations of positional numeral systems
Some numbers cannot be represented using a finite sequence of fractional digits , in a positional numeral system .
Irrational numbers , such as pi , simply cannot
be represented using a finite sequence of digits , in a positional numeral system .
Rational numbers of the form p/q , cannot be
represented using a limited sequence of fractional digits such as .12 , when the chosen base
, or the base multiplied by 1,2 ... q-1 is not divisible by q .
As an example 1/4 can be represented in the decimal positional numeral
system , because 10 * 2 is divisible by 4 , as such
1/4 can be written in the decimal positional numeral system , as 0.25 .
1/3 is representable in the ternary positional numeral system , because when
borrowing in this case , we are borrowing multiples of 3 , so 1/3 can be written as
0.1 , in base 3 .
1/3 has a repeating representation in the decimal positional numeral system
, because 10 * 1 , and 10 * 2 are not divisible by 3 . As such
1/3 is represented in the decimal positional numeral system , as the repeating sequence
0.33333... .
It can be proven that any repeating fractional number , can be written as a rational number , for example :

Problems arise , when limiting the fractional part of a number in a positional numeral system , to a limited number of digits .

When the number of digits is limited , this means that only a limited number of fractional values can be generated . The question hence to ask , is how to represent non generated fractional values , is it by one of the generated values , or by just stating it cannot be represented .
Let’s take as an example , the set of fractional parts generated in base 2 , when limiting the number of fractional bits to three .

0.1 in base 10 , has the following representation in base 2 .

0.1 is smaller than any nonzero value , in the selected base 2 subset , which
has a limited number of fractional digits , as such it cannot be represented in this subset . This is
called an underflow .
Larger values , such as values larger than 0.1 , and which are not present in the generated
set , can only be represented by approximation . 0.4 for example , can be represented as
.011 which is equal to 0.375 in decimal . The difference between
the stored value , and the actual value is as such : 0.4 - 0.375 , which is
equal to 0.025 .
The stored value of 0.77 , when subtracted from the stored value of 0.57 , is
equal to .110 - .100 , which is equal to .010 . The stored value of
0.3 is .010 , as such in our representation of the fractional parts in base 2 ,
0.77 - 0.57 is equal to 0.3 and is not equal to
0.2 .
Adding more bits to the fractional part , will improve the
precision of the represented numbers , and of the calculations . For example , when
4 bits are used for the fractional part , 0.1 in decimal can be represented as
0.0001 in binary .
Even with a wider number of digits , the problems discussed earlier will always persist . Some numbers cannot be represented accurately using a limited number of digits , such as the irrational , and having a limited number of digits , a limited number of fractional parts is available, as such a limited precision .
IEEE floating point format
When using the IEEE floating point number representation , in addition to the precision , which is the number of bits selected for the fractional part , there is the sign bits , and the exponent bits .
What this means , is that additional values can be generated , because of the presence of the exponent , and the sign bits , so simply put , this is just a way to improve the precision .
An IEEE floating point number , has a bit representation , and a numerical value . The IEEE specified the bit format that a floating point number must have , and by which its numerical value is to be interpreted . This bit format can be put to work or accustomed to different word length . A word is formed of a number of bits , so this format can be put to work on 32 bits , 64 bits , 128 bits and so on … It just works the same.
A single precision floating point number has a 32 bit representation , a double precision floating point number has a 64 bit representation , and a quadruple precision floating point number has a 128 bits representation .

Infinite values
When the exponent bits are set all to 1 , and the precision bits
are set all to 0 , the floating point number bits sequence , represent an infinite value .
There are two infinite values , positive and negative infinity
. When the sign bit is 0 , this is positive infinity , when the sign bit is 1 ,
this is negative infinity .

Infinity can be caused for example , when dividing a nonzero
number by 0 , or when the result of an operation , after rounding has the infinite value .
Not A Number value
When the exponent bits are all set to 1 , and the precision bits
are set to anything but 0 , the bit sequence , of the floating point number ,
represents NAN .
The value NAN , means not a number , and it can happen
for example , when dividing 0 by 0 , or when adding positive and
negative infinity .
There is no negative or positive NAN , so the sign bit does not matter .

Denormalized values
When the exponent bits are all set to 0 , the floating point
number is in what is called a denormalized form .

The rational value of the floating point number , is equal ,
to the sign value , multiplied by 2 to the exponent value , multiplied by the precision value
.

The sign value is either 1 , if the sign bit value
is 0 or -1, if the sign bit value is 1 .
The exponent value is calculated using the formula
1 - bias . The bias is calculated using the formula :

The precision value is the same as the precision bits value . The precision bits value is calculated as a fractional positional binary number .
To illustrate this , let us say , that the floating points are
encoded using 7 bits . 1 bit is a sign bit , 3 bits are exponent bits , and 3
bits are precision bits .
The sign value is equal to 1 , when the sign bit
is 0 , and to -1 when the sign bit is 1 .
The exponent value is equal to 1 - bias , which is
equal to -2 .

The precision bits values are , calculated as positional binary fractions .

The precision values are the same as the precision bits values .
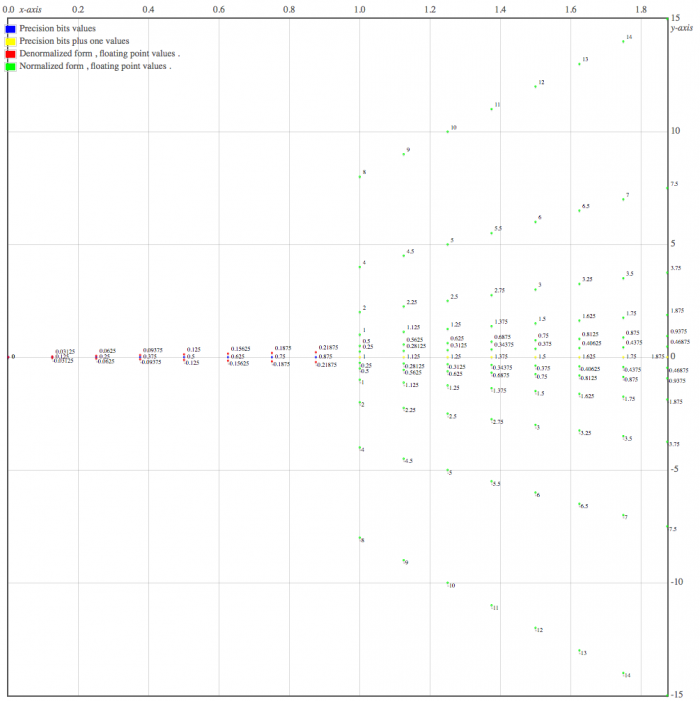
As such when in denormalized form , the 7 bits floating point
numbers , possible rational values are :

Normalized values
When the exponent bits are not all set to 0 , or
are not all set to 1 , the floating point number bits , are in normalized form .

The floating point number rational values , are equal to the sign value , multiplied by two to the power of the exponent value , multiplied by the precision value .

The sign value , is equal to 1 , when the sign bit
is 0 , and is equal to -1 , when the sign bit is set to 1 .
The exponent value , is equal to the exponent bits values , minus the bias . The exponent bits values , are calculated , as if the exponent bits are in the binary positional numeral system . The bias is calculated as it was calculated in denormalized form .

The precision values , is equal to one , plus the precision bits values . The precision bits values , are calculated as if the precision bits , are a fractional base two number .
To illustrate this , let’s say that the floating point
number is encoded using 7 bits . 1 bit is used for the sign , 3
bits are used for the exponent , and 3 bits are used for the precision .
The sign value is equal to 1 , when the sign bit
is 0 , and -1 when the sign bit is 1 .
The possible exponent values are :

The possible precision values are :

The 7 bits floating point number , possible normalized form rational
values are :

Visualizing floating points possible values , when the encoding is done on 7 bits
Commutativity , associativity , and distributivity
IEEE floating point addition
commutative : a + b = b + a
not associative : ( 5 + 1e40 ) - 1e40 != 5 + ( 1e40 - 1e40 )
because 0 != 5
IEEE floating point multiplication
commutative : a * b = b * a
not associative : 1e40 * ( 1e300 * 1e-300 ) != ( 1e40 * 1e300 ) * 1e-300
because 1e40 != Infinity
not distributive over addition and subtraction
0 * (1e308 + 1e308 ) != ( 0 * 1e308 ) + ( 0 * 1e308 )
because NaN != 0
1e30 * ( 1e300 - 1e300 ) != 1e30 * 1e300 - 1e200 *1e300
because 0 != NaN
IEEE floating point division
not commutative : ( 1.0 / 2 ) != ( 2.0 / 1 )
not associative : ( 1.0 / 2 ) / 3 != 1 / ( 2.0 / 3 )
because 0.1666 != 1.5
IEEE floating point subtraction
not commutative : 1.0 - 2 != 2 - 1.0
not associative : -4 - ( -4 - -3.0 ) != ( -4 - -4.0 ) - -3
-4 - ( -4 - -3 ) = -4 - -1 = -3
( -4 - -4 ) - -3 = 0 - -3 = 3
Floating points format in C
Floating point formats are used to represent real , or rational numbers , in
the computer . The C standard has three data types to be used with a floating point
standard , they are : float , double , and long double .
The c standard , does not specify which floating point standard
is to be used , but usually , the IEEE floating point format is used , as such float is
mapped to the IEEE single precision floating point format , and double is mapped to the IEEE
double precision floating point format .
By default a floating point literal such as 1.0 , has the type
double , unless suffixed with f , in which case it will have the type
float , or suffixed with l , in which case it will have the type
long double .
To detect if a floating point value is NaN , it
can be done by using the isnan function , and to detect if a floating point number is
infinity it can be done using the isinf function .
The isnan , and isinf functions are both defined in the math.h
header .
#include<stdio.h>
#include<math.h>
int main ( void ){
printf( "%d\n", isnan( 0.0/0.0 ) );
/* 0.0 divided by 0.0 , results in
not a number , as such isnan
returns a nonzero value . */
// Output : 1
printf( "%d\n" , isinf( 1.0/0.0 ) );
/* 1.0 divided by 0.0 results in
+ infinity , as such isinf
returns a nonzero value */
// Output : 1
}